【翻译】Core Animation 3D 绘图（上）

发表于 更新于 阅读次数： 阅读次数：

这是关于 Core Animation 三维绘图的翻译文第一篇（共两篇），主要讲了 iOS 中做三维变换时所需要用到的一些基础知识，原文是 Think & Build 上的 Introduction to 3D drawing in core animation (Part 1)。
想要把玩一下完整项目的话，可以去原文中的 Github 地址中看看，不过文中附带的代码已经是项目中最核心的部分了，组合起来也可以得到一样的效果。

因为翻译这篇文章的时间已经比较久远了，难免有一些错误的地方，欢迎大家指出来共同进步。

Core Animation 可以让我们在不直接使用 OpenGL 的情况下实现某些 3D 效果，但是相对的，使用 Core Animation 来写一个复杂的 3D 游戏就不是那么明智了。

这一部分的文章将会探讨一下简单的 3D 绘图的理论，并且构建一个简易的 3D 场景。
下一部分的文章将会用 Core Animation 来创建一个更复杂一些的 3D 场景。

要是想把这些代码跑起来的话，首先要记得将 QuartzCore 框架添加到项目中。

3D 和 矩阵（外加一点点数学运算…）

在三维空间绘图，意味着我们需要在传统的二维空间坐标系中加入一个深度，也就是我们高中数学中的 Z 轴。

在这个全新的坐标系中，通过改变 X、Y 和 Z 坐标的数值，我们可以将物体水平、垂直和远近移动（想象你在看着手机屏幕，距离你的脸越近的物体 Z 值越大）。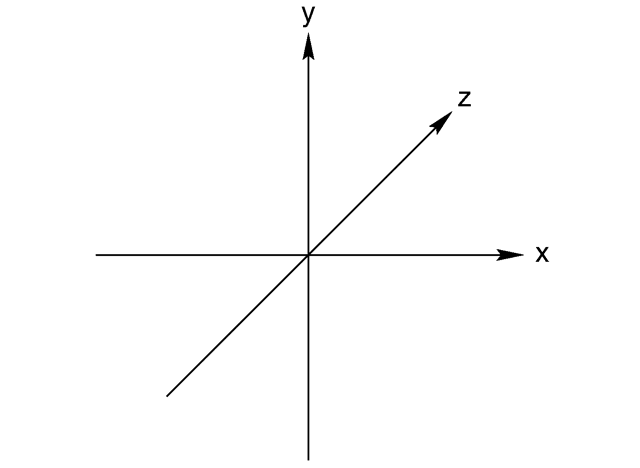
handed

无论在二维还是三维空间中，要让物体产生位移或形变，比如移位、缩放和旋转，都需要经过一点数学运算。
使用矩阵是做这些运算最合理的方式。

简单来说，矩阵就相当于多维数组。
举个例子，在三维空间中，我们会使用一个 4x4 的矩阵来表示坐标：

[X][0][0][0]
[0][Y][0][0]
[0][0][Z][0]
[0][0][0][1]

把这个矩阵跟对象每一点的坐标相乘，我们就可以让这个对象发生位移或形变。
再准确一些，这个矩阵是一组比例系数。通过它，按比例地改变每一条坐标轴上的数值，以达到缩放这个对象的目的。
同理，如果想要实现其他效果，例如旋转和位移，那么你只要改变一下上述矩阵中的数值就可以了。
headscratch

莫慌！你不需要完全弄懂这些原理性的东西，而且你也基本不会直接用到。Core Animation 已经像一个黑盒一样帮你完成了这一切。

话说回来，了解一下代码底层到底在做些什么总归是好的。如果你想要更详细地学习一下关于矩阵的一切，可以参考这篇文章。

三维变换

现在你已经对三维空间和矩阵的作用有了一些概念，是时候用 Core Animation 创建一些东西了。
下面有几个准备好了的方法，分别会做一些不同的事情，我们一个个来看。

A_singlePlane 实现了一个绕Y轴旋转了45度的圆角矩形。

首先，我们创建一个 CALayer 来作为接下来的一切操作的容器（虽然不是必须的，但是感觉要比直接在一个 view 的 layer 上面操作要好）。

1
2
3
4
5
6
- (void)A_singlePlane{
    // Create the container
    CALayer *container = [CALayer layer];
    container.frame = CGRectMake(0, 0, 640, 300);
    [self.view.layer addSublayer:container];
}

接下来我们创建另一个 CALayer，一个圆角矩形。

1
2
3
4
5
6
//Create a Plane
CALayer *purplePlane =
	[self addPlaneToLayer:container
	size:CGSizeMake(100, 100)
	position:CGPointMake(100, 100)
	color:[UIColor purpleColor]];

这里用到了一个工具方法，只是单纯的创建一个 CALayer，加到 container 当中，然后返回这个 CALayer。代码非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- (CALayer *)addPlaneToLayer:(CALayer*)container size:(CGSize)size position:(CGPoint)point color:(UIColor*)color {
    //Initialize the layer
    CALayer *plane = [CALayer layer];

    //Define position,size and colors
    plane.backgroundColor = [color CGColor];
    plane.opacity = 0.6;
    plane.frame = CGRectMake(point.x, point.y, size.width, size.height);
    plane.borderColor = [[UIColor colorWithWhite:1.0 alpha:0.5]CGColor];
    plane.borderWidth = 3;
    plane.cornerRadius = 10;

    //Add the layer to the container layer
    [container addSublayer:plane];

    return plane;
}

最后我们用 CATransform3D 来完成这个变换。
什么是 CATransform3D？Cmd + click 这个数据类型，你会发现这是一个结构体，代表着一个有点奇怪的矩阵：

1
2
3
4
5
6
7
8
9
struct CATransform3D
{
  CGFloat m11, m12, m13, m14;
  CGFloat m21, m22, m23, m24;
  CGFloat m31, m32, m33, m34;
  CGFloat m41, m42, m43, m44;
};

typedef struct CATransform3D CATransform3D;

真正产生变换作用的代码也是非常简单：

1
2
3
4
//Apply the transform to the PLANE
CATransform3D t = CATransform3DIdentity;
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 1, 0);
purplePlane.transform = t;

首先用 CATransform3DIdentity 来初始化一个 CATransform3D，这个 CATransform3DIdentity 相当于是一个空值。然后我们通过 CATransform3DRotate 这个方法来完成前面提到过的“与旋转矩阵相乘”这个步骤。

这个方法需要几个参数：一个初始矩阵、旋转角（弧度制）和三个坐标轴的影响系数（表示产生多少作用的一个比例系数）。在这个例子中，X 和 Z 轴没有被影响到，而 Y 轴是完全被影响…简而言之，这个对象最后是绕着Y轴旋转了 45 度。

下图就是这个例子的最终效果：
pa1

嗯…？它完全不像一个三维图啊！我们只看到了一个沿着 X 轴压缩了一点的矩形。

问题在于我们没有设置它的 **透视数值( perspective value )**。通常我们会用正面投影的方法来实现平面上的三维画面，但是这样产生的是一个变平了的三维图像。换句话说，用了正面投影之后，你就难以察觉 Z 轴变化带来的景深变化了。

为了给我们的画面添加景深，我们要调整变换矩阵的 m34 数值，这个变量决定了视图的透视值。
代码跟前面的很像，只有变换的部分有些不同：

1
2
3
4
5
6
//Apply transformation to the PLANE
CATransform3D t = CATransform3DIdentity;
//Add the perspective!!!
t.m34 = 1.0/ -500;
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 1, 0);
purplePlane.transform = t;

我们可以像这样直接改变 m34 属性的值。
就不继续深入研究这个值带来的数学上的影响了，但是要大概明确一点，这个值越接近于零，透视就越明显。
下面是不同 m34 值对应的不同结果：
pa2_1
pa2_2

三维变换链

为了给单一的对象套上不止一种变换，我们可以通过矩阵相乘的方式来实现。

举个例子，如果我们想同时把对象旋转一下并移开一点，我们可以这样构造我们的变换矩阵：

1
TransformMatrix = TranslateMtx * RotateMtx

在数学上，乘法是满足交换律的，但是矩阵相乘 不满足交换律！也就是说，AxB 不等于 BxA。这一点必须要牢记在心！

下面这个例子中，我们会对两个不同的对象施以相同的变换，但是变换的顺序不一样。看看主要的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//Apply transformation to the PLANES
CATransform3D t = CATransform3DIdentity;

//Purple plane: Perform a rotation and then a translation
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 0, 1);
t = CATransform3DTranslate(t, 100, 0, 0);
purplePlane.transform = t;

//reset the transform matrix
t = CATransform3DIdentity;

//Red plane: Perform translation first and then the rotation
t = CATransform3DTranslate(t, 100, 0, 0);
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 0, 1);
redPlane.transform = t;

看看结果：
pa3

瞧瞧，不一样了吧。

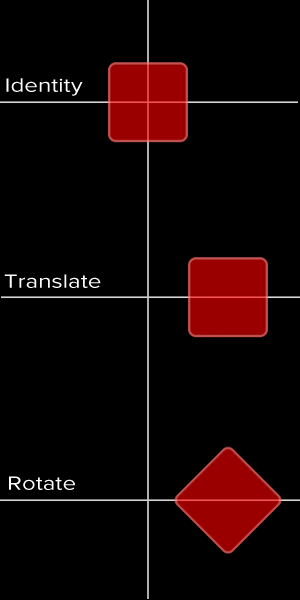
来看看紫色的方块：我们先对它进行了一次旋转变换，这引起了它坐标系的旋转。
下一步，我们改变了紫色方块的 X 坐标，这一改变是在新坐标系上进行的，所以结果就是跟红色方块不一样了。

下面的图片应该可以让你有一个更形象的概念：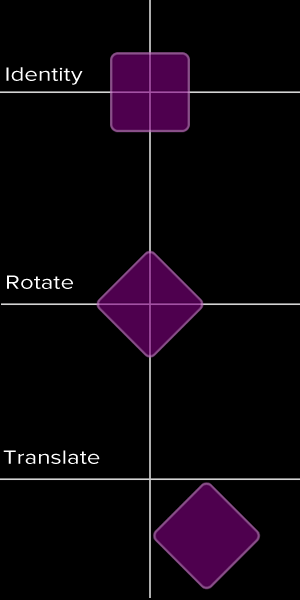
pa4
pa5

图层层次（Layer Hierarchies）是个啥？

不知道你注意到了没，到现在为止，我们都是直接对这些方块对象实施变换的。在一个三维场景中，通常是创建一组对象，组成一个带有层次感的画面，然后对层次的根对象进行变换。

再举个栗子。

我们把 4 个方块加入到容器里面。
不进行任何变换，看起来就像这个样子：
pa6

接着，对每一个方块都进行一次绕 Y 轴的旋转，我们会看到如下画面：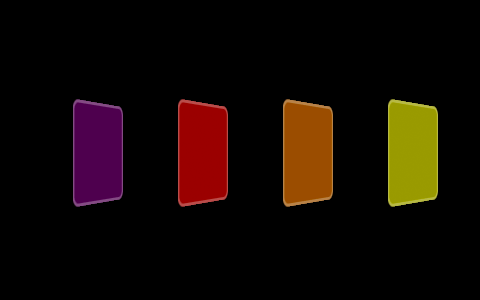
pa7

然而，如果这个变换是直接作用在容器图层上的，景色又完全不同了：
pa8

我们可以把最后面这幅图看作是摄像机位置的改变。也就是说，我们没有移动这些方块，而是我们的视角改变了。

上述的两种变换对应下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//Transformation
CATransform3D t = CATransform3DIdentity;

BOOL applyToContainer = NO;

//Apply the transformation to each PLANE
if(!applyToContainer){
    t.m34 = 1.0 / -500.0;
    t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
    purplePlane.transform = t;

    t = CATransform3DIdentity;
    t.m34 = 1.0 / -500.0;
    t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
    redPlane.transform = t;

    t = CATransform3DIdentity;
    t.m34 = 1.0 / -500.0;
    t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
    orangePlane.transform = t;

    t = CATransform3DIdentity;
    t.m34 = 1.0 / -500.0;
    t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
    yellowPlane.transform = t;
}

//Apply the transformation to the CONTAINER
else{    
    CATransform3D t = CATransform3DIdentity;
    t.m34 = 1.0/-500;
    t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
    container.transform = t;
}

来认识一下 CATransformLayer

目前为止一切看起来都很顺利。不过，其实 CALayer 并不适合作为三维图层层次的根。

来看看为什么。

现在我们创建 4 个 X、Y 坐标都一样的方块，唯一不同的是它们的 Z 坐标。
紫色方块是距离你最近的，黄色方块时距离你最远的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Apply transforms to the PLANES
t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -10);
purplePlane.transform = t;

t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -50);
redPlane.transform = t;

t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -90);
orangePlane.transform = t;

t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -130);
yellowPlane.transform = t;

然后，我们像之前那样让整个容器旋转一下。

1
2
3
4
5
//Apply transform to the CONTAINER
CATransform3D t = CATransform3DIdentity;
t.m34 = 1.0/-500;
t = CATransform3DRotate(t, 80.0f * M_PI / 180.0f, 0, 1, 0);
container.transform = t;

是不是觉得应该要看到这个场景：
pa9

但结果却是：
pa10

这是因为，CALayer 并不能处理三维图层层次的景深，所以它只是把所有的东西在同一个 Z 平面上压扁了。

为了达到预想的效果，我们要用 CATransformLayer 来作为根对象。

Bug fixed:

1
2
3
4
//Create the container as a CATransformLayer
CATransformLayer *container = [CATransformLayer layer];
container.frame = CGRectMake(0, 0, 640, 300);
[self.view.layer addSublayer:container];

要记住，CATransformLayer 是一个特殊的图层，与 CALayer 非常不同的是，它只会渲染自己的子图层，而 backgroundColor、contents、border 等等这些属性则会被完全忽略掉。

总结

那么第一部分的内容翻译就到此为止了，下半部分也会在整理好之后的第一时间放出来。建议大家去玩玩这些代码，最好试试看上面没有提到的 CATransform3DScale 咯。

再一次附上原文：Introduction to 3D drawing in core animation (Part 1)